1.4.i. G0, G1, G2, G3
Der Begriff der Stetigkeit ist in der Mathematik von großer Bedeutung. Dabei wird eine Funktion als stetig bezeichnet, sobald eine hinreichend kleine Änderung des Argumentes der Funktion zu kleinen Änderungen des entsprechenden Funktionswertes führen. Dies bedeutet insbesondere, dass in der Funktion keine Sprünge vorliegen.
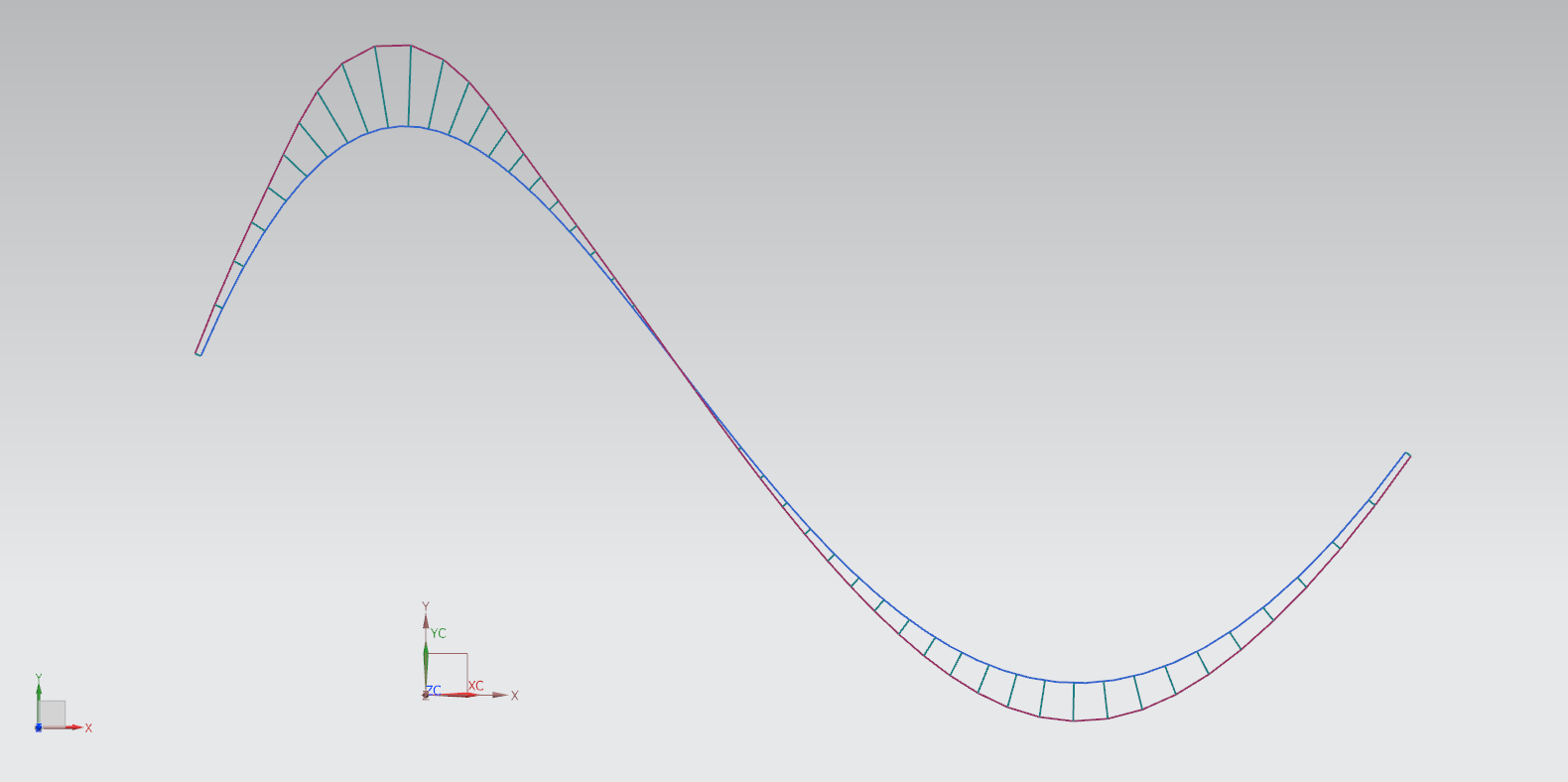
Auch NX9 bedient sich dem Konzept der Stetigkeit, um Übergänge zwischen Kurven zu charakterisieren. Hierbei treten die Bezeichnungen G0, G1 und G2 auf, welche den Übergang von einer Kurve bzw. einer Fläche in die nächste beschreiben. Um die Krümmung mithilfe einer optischen Analyse sichtbar zu machen, werden sogenannte Krümmungskämme eingesetzt. Die Länge der Stacheln der Kämme ist ein Indikator für den Krümmungsradius der Kurve an der jeweiligen Stelle.
Die nachfolgende Abbildung zeigt eine Spline-Kurve, deren Krümmung durch
Krümmungskämme (engl. combs) sichtbar gemacht wurde. Mittels Rechtsklick auf die jeweilige Kurve kann die Funktion Combs aufgerufen werden.
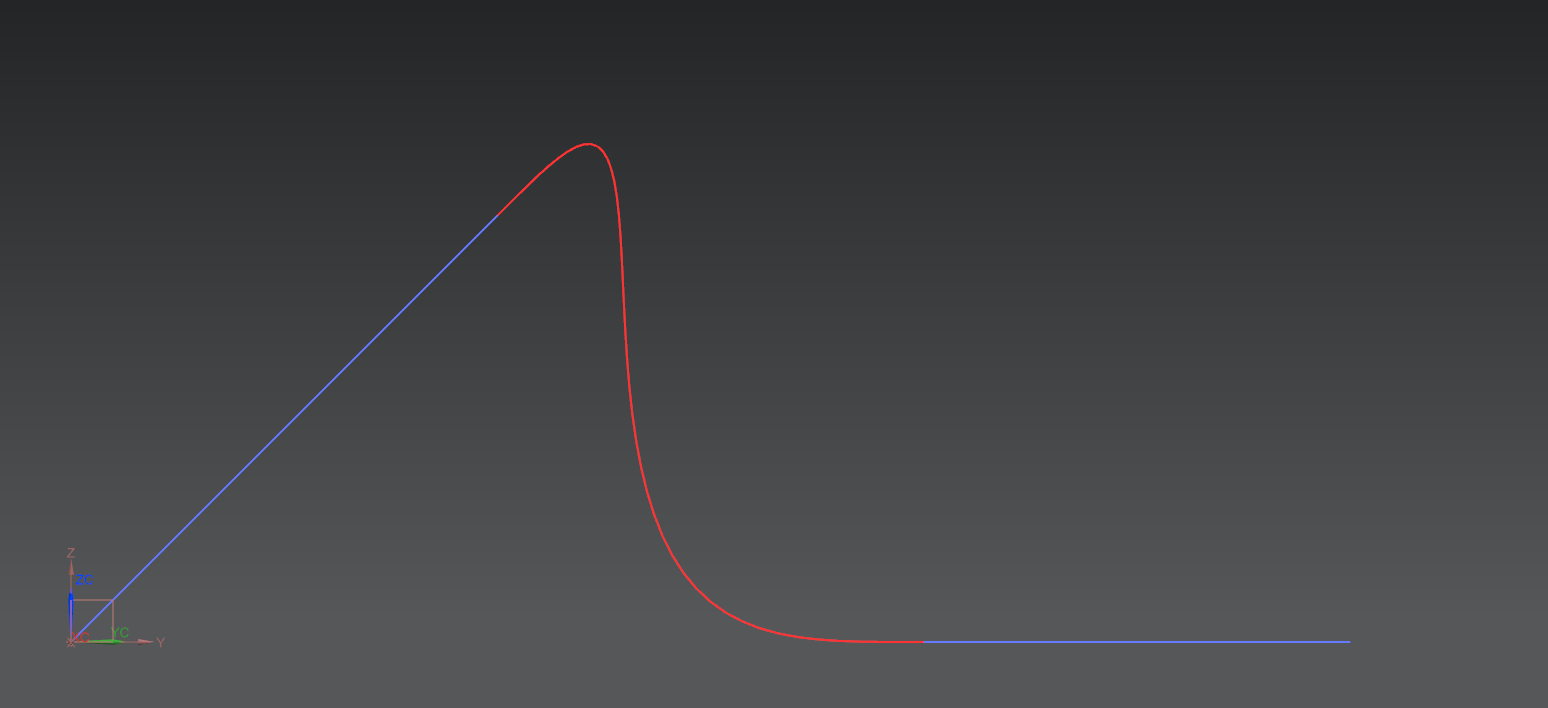
Um die genannten Zusammenhänge der Stetigkeiten näher zu erläutern sollen als Beispiel zwei
Kurven dienen, die mithilfe einer dritten Kurve verbunden werden.
Dazu wird die Funktion Bridge Curve verwendet. Diese Funktion erlaubt es, den Grad der Stetigkeitsübergänge zu wählen.
Stetigkeit: G0
Werden die Geraden durch eine G0-stetige Kurve verbunden, so treten zwar keine Lücken auf,
jedoch ist ein deutlicher Knick im Verlauf der gesamten Kurve zu erkennen. Das bedeutet, dass die Kurven an dieser Stelle nicht tangentenstetig sind. Für die Freiformkurven- und Freiformflächenmodellierung bedeutet dies einen kantigen Kurven- bzw. Flächenzug und damit Einbußen im Bereich der Qualität und Ästhetik.
Tangentenstetigkeit: G1
Um dem Problem der G0-Stetigkeit entgegenzuwirken, kann die Tangentenstetigkeit G1
herangezogen werden. Hierbei erfolgt eine Glättung der Übergänge der Kurven, d.h. ihre Winkel zueinander entsprechen exakt 180°. Die Glättung wird erzielt, indem die Richtungen der Tangentenvektoren angeglichen werden. Dennoch können diese Übergänge abrupt erfolgen, was sich in der Ausbildung der Krümmungskämme bemerkbar macht. Tritt dies bei Flächen auf, so sieht der Betrachter eine Kante, obwohl der Übergang G1-tangentenstetig ist. In diesem Fall spricht man von sogenannten Lichtkanten.
Krümmungsstetigkeit: G2
Um die oben erwähnten Lichtkanten zu vermeiden, können die Übergänge zwischen den Kurven als
G2-krümmungsstetig ausgeführt werden. Das Resultat ist ein optisch sanfterer Übergang, d.h. eine stärkere Ausprägung der Glättung als bei der G1-Tangentenstetigkeit. Dies erkennt man ebenfalls an der Ausprägung der Krümmungskämme. An den Übergängen haben die Stacheln dieselbe Länge, dass heißt, dass der Krümmungsradius ist an dieser Stelle identisch ist. Hierbei sei angemerkt, dass G2-krümmungsstetig ausgeführte Kurvenzüge ebenfalls tangential sind und unter optischen Kriterien ein höheres Maß an Qualität aufweisen, als G1-tangentenstetige Kurven. Allerdings ergibt sich das Problem, dass diese Übergänge nicht immer realisierbar sind.
Um die Übergänge noch sanfter zu gestalten, kann die G3-Variante herangezogen werden. Die Übergänge der Krümmungskämme der Kurven werden ebenfalls sanfter und die durch die
Stachelspitzen definierte Kurve ist nun wiederum eine Kurve, die ohne scharfe Kanten oder Knicke verläuft. Im Sinne der optischen Betrachtung ist die G3-Variante höherwertiger als die G2-Krümmungsstetigkeit.
Dieser Sachverhalt soll an dieser Stelle noch einmal kurz aufbereitet werden.
Wie bereits erwähnt wird mithilfe der Bridge Curve Funktion eine Kurve als Verbindungsstück zwischen die beiden Geraden gelegt. Bei dieser Kurve handelt es sich um eine Spline-Kurve, die hier vorab schon einmal näher erläutert werden soll:
Die Spline-Kurve ging aus der Anforderung hervor, beliebig gekrümmte Kurven und Flächen modellieren zu können, die zudem „glatt“ erscheinen, d.h. keine Unstetigkeiten im Kurvenverlauf aufweisen. Mit den herkömmlichen Interpolationsverfahren, wie z.B. Lagrange-Polynome, Newton-Polynome oder die Hermite-Interpolation, war es nicht möglich, eine solch komplexe Geometrie darzustellen. Daraus entwickelte sich der Ansatz, den Kurvenzug in einzelne Kurvensegmente zu zerlegen. Bei der Zusammensetzung der Kurvensegmente ist ein einfacher stetiger Übergang nicht ausreichend, zwar wären dann alle mit einander verbunden, jedoch kann die Forderung nach glatten Übergängen nicht gewährleistet werden. Aus diesem Grund müssen die Kurvensegmente nicht nur stetig sein, sondern es muss zusätzlich verlangt werden, dass die erste Ableitung oder allgemein die ersten k-Ableitungen stetig ineinander übergehen. Ein Kurve, die diese Anforderungen erfüllt, wird Spline-Kurve genannt. Eine Spline-Kurve vom Grad n ist demnach n-1 mal differenzierbar.
Diese Eigenschaft kann man anhand der zuvor beschriebenen Kämme sichtbar machen, deren Funktion den Verlauf der Krümmung beschreiben. Werden zwei Kurven nur über die G1-Stetigkeit miteinander verbunden, so laufen diese zwar tangential ineinander über, jedoch ergibt sich kein stetiger Übergang der Krümmung an dieser Stelle. Es entsteht ein Sprung im Krümmungsverlauf, da diese Kurve nur einmal stetig differenzierbar ist. Wird der Grad des Kurvensegments erhöht, so ist diese öfter stetig differenzierbar. Das heißt, der Grad der Ableitung ist ebenfalls höher. Da diese Ableitungen der Kurvensegemente stetig miteinander verbunden sind, wird deutlich, dass der Übergang mit der Erhöhung des Grades der Kurve sanfter wird.
Im Kapitel 5 wird im Rahmen der Analysetools von Kurven noch einmal näher auf die Kämme eingegangen.
Aufgabe: G0,1,2,3-Stetigkeit
Zum besseren Verständnis sollen Sie nun zwei Kurven mithilfe der Funktion Bridge Curve miteinander verbinden.
Insert > Curve from Curves > Bridge Curve
Wenn Sie die Funktion Bridge Curve geöffnet haben, können sie unter den Reitern Start und End den Grad der Stetigkeit am Beginn und am Ende der Kurve bestimmen. Dadurch sind auch Kombinationen der Stetigkeiten möglich, wie beispielsweise ein G0-stetiger Übergang am Start und ein G2-stetiger Übergang am Ende der Kurve.
Wählen Sie für die Übergänge unterschiedliche Stetigkeiten aus und machen Sie das jeweilige
Ergebnis über die Funktion Combs zur Darstellung der Krümmungskämme sichtbar.